Light (electromagnetic radiation) is incident on a silver plate. What is the threshold frequency of the light in order for electrons to be freed in the sliver? If light with twice the threshold frequency strikes the plate, what is the maximum kinetic energy of the freed electrons? What is the speed of the electron in this case? What will happen if visible light strikes the silver?
-
In introduction to quantum mechanics units, you are introduced to a variety of experimental results involving light, atoms, or constituents of atoms. In most cases, when you look at interactions on these tiny scales, you have a foundations of quantum mechanics problem.
In this case, the interaction of interest is that of light (electromagnetic) energy being used to free electrons from their atoms. This is known as the photoelectric effect. The photoelectric effect is best understood through Conservation of Energy—tracking the energy of the incoming light as it is transferred to the electron—so at root this is an energy problem.
In quantum mechanics problems, light is sometimes considered as a wave and sometimes as a particle.
protons, neutrons or electrons
-
In the photoelectric effect, the energy from incident light is absorbed by electrons—freeing them from their atoms and (if additional energy is available) giving them kinetic energy. This is one of the few cases where a picture is not particularly helpful in understanding the problem.
One of the keys to the photoelectric effect is that the amount of current produced is best understood by treating light as photons. Therefore, I drew light as a photon striking the sliver plate.
Photoelectric interactions are understood as the energy of a single photon absorbed by a single electron, freeing it from its atom.
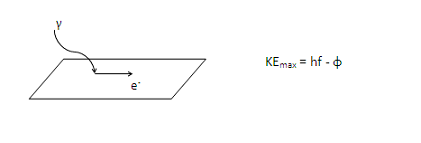
Photoelectric effect problems are best understood through energy. Your book as probably provided you with this partially-solved version of the Conservation of Energy equation.
Where did you get this equation? It doesn’t look like the photoelectric equation in my book?
Some books us K instead of KE (or omit the subscript “max”) for kinetic energy, and others use W instead of φ for the work function. Although they may look different, these are all the same equation. For example, KEmax = hf – φ may also be written as Kmax = hf – W.
Some books us K instead of KE (or omit the subscript “max”) for kinetic energy, and others use W instead of φ for the work function. Although they may look different, these are all the same equation. For example, KEmax = hf – φ may also be written as Kmax = hf – W.

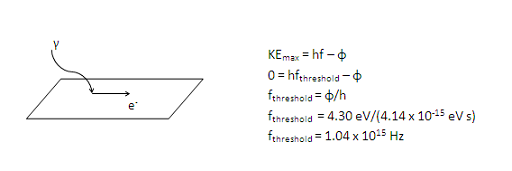
Note that visible light (part 4 of this problem) has a maximum frequency of 7.5 x 1014 Hz, which is less than the threshold frequency for silver. In other words, visible light does not have enough energy to free an electron, so nothing happens when visible light strikes silver. Once you understand threshold frequency, scroll down to answer the remaining questions in this problem.
No numerical information was given in this problem. How do I begin?
In the photoelectric effect, photon energy is absorbed the an electron. That energy is used to free the electron from the atom. If the photon has more energy than is required to free the electron, the additional energy goes to kinetic energy of the photon.
At the threshold, the photon has just enough energy to free the electron and there is none left for kinetic energy. In other words, KE = 0.
The work function, or the amount of energy needed to free an electron from an atom, depends on the photoelectric material. If it is not given in a problem, you can find it tabulated in your book or on the web.
What is an eV?
An eV (electron volt) is the unit of energy given to one electron that has been accelerated through a potential difference of 1 Volt. It is equal to 1.6 x 10-19 J. Because the value for work function that I found was given in eV, I made sure to use Planck’s Constant (h) also in eV.
In the photoelectric effect, photon energy is absorbed by an electron. That energy is used to free the electron from the atom. If the photon has more energy than is required to free the electron, the additional energy goes to kinetic energy of the photon.
At the threshold, the photon has just enough energy to free the electron and there is none left for kinetic energy. In other words, KE = 0.
The work function, or the amount of energy needed to free an electron from an atom, depends on the photoelectric material. If it is not given in a problem, you can find it tabulated in your book or on the web.
An eV (electron volt) is the unit of energy given to one electron that has been accelerated through a potential difference of 1 Volt. It is equal to 1.6 x 10-19 J. Because the value for work function that I found was given in eV, I made sure to use Planck’s Constant (h) also in eV.
Three significant figures were given in the information used for this problem, so three significant figures are included in the solution.
1 Hertz (Hz) = 1 s-1
According to your text or a web search, 7.5 x 1014 Hz is the frequency of violet light. Remember that red light has the lowest photon energy (longest wavelength, lowest frequency) of the visible spectrum, and violet light has the highest.
----------------------------------------------------------------------------------------------
Step 2

In the second question, you are told the frequency (and therefore the energy) of the incident photon, so it is straightforward to solve for the maximum kinetic energy of the electron. Note that this problem could also have been solved conceptually—you know that you have twice as much energy as is needed to free the electron, so half of the energy (4.30 eV) goes to freeing the electron and the remaining half (also 4.30 eV) is available as kinetic energy.
Now that you know the kinetic energy of the electron, it is merely a definition problem to find its speed.
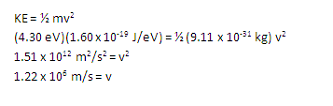
The frequency of the incident photon is twice the threshold frequency, or 2 x (1.04 x 1015 Hz).
In order to find velocity, you need to work in MKS units, so make sure to convert energy from eV to J.
In this case, you are relating the velocity and kinetic energy of the electron, so make sure to use the mass of an electron.
Because photon energy is directly proportional to frequency (E = hf), if you double the frequency of light you double the photon energy.
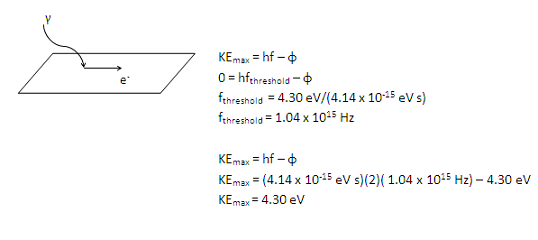
Once you recognize this problem as the photoelectric effect, you can solve it mathematically merely by plugging into KEmax = hf – φ. However, to understand the problem you need to recognize that this equation tracks energy.
Remember that in order to understand the experimental results of the photoelectric effect, we treat light as a particle rather than as a wave. In other words, we understand the interaction of light with the photoelectric material as interactions between a single photons and a single electrons. If the initial energy of a photon (hf) is at least enough to free an electron (φ) it will do so. If there is additional energy left over (if hf – φ is greater than zero), that remaining energy goes to kinetic energy of the electron.
Why do you refer to both “light” and “electromagnetic radiation”?
Light is electromagnetic radiation. However, in common language we typically use the word “light” to refer to visible light only, whereas to a physicist “light” refers to the entire electromagnetic spectrum. I used both terms to avoid confusion but also to call attention to the difference in use.
What do you mean by “threshold frequency”?
Threshold frequency is the lowest frequency of light that will free electrons in any given material. This makes more sense once you recognize this as a photoelectric effect problem.
