Wave Physics Problems
One of the key properties that defines waves is interference. In some cases, interference can give rise to standing wave patterns. (Note that in two dimensions, we refer to these standing wave patterns as interference and diffraction patterns.) The wave properties of reflection and refraction and their applications to optics are also addressed in this section.
How to Solve Standing Wave Problems
-
1.Identify the Problem
Whenever two waves of the same type are in the same place at the same time, they interfer with each other. This might happen when two waves are created and overlap, or when one wave reflects off of a new material (the reflected wave traveling in one direction interfers with the initial wave traveling in the other direction.) Standing waves are created when the waves always cancel in some places. In most problems, key words like "standing wave," "interference pattern," "diffraction pattern," or "thin film" will initially tip you off to approach the problem through standing waves. This is also the physics behind musical instruments.
-
2. Draw a Picture
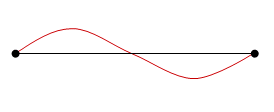
The purpose of the picture in one dimensional standing waves is to help you relate the wavelength of the wave to the physical parameters of the situation--for example, to the length of the musical instrument. Begin by identifying the boundary conditions (node or anti-node at each end) for the wave and draw the simplest wave pattern that meets those boundary conditions. Additional standing wave patterns are obtained by adding additional nodes along the length of the resonant column or string.
The purpose of the picture for two dimensional standing waves is to visualize the geometry of the situation. Draw the wave or waves as they are created at the source and draw the screen on which you see the pattern. The reference line for θ is the line straight down the middle, from the source to the screen, and θ identifies the angular position of each maximum or minimum from that center line.
-
3. Select the Relation
In one dimension, you typically want to relate the frequency of the wave to other wave properties. To do this, you simply need the wave equation: v = f λ.
In two dimensions, you will generally relate the location of maxima and minima to wave properties and the geometry of the experimental apparatus. The equations for a single opening (diffraction) problem are D sinθ = (m + 1/2)λ for a maximum and D sinθ = m λ for a minimum. The equations for a double slit interfence problem are d sinθ = m λ for a maximum and d sinθ = (m + 1/2)λ for a minimum.
For thin film interference patterns, use 2 t = m λ/n and 2t = (m + 1/2) λ/n. You need to understand the reflective properties of the situation to determine which equation gives constructive interference and which gives destructive.
-
4. Solve the Problem
As long as you understand the meaning of the symbols, solving standing wave problems is straightforward. If your problem refers to quantities that are not part of the equation--for example, the distance to a screen or the length of a guitar string--use your picture and perhaps trigometric relationships to relate the given and calcuated quantities to those that are requested.
-
5. Understand the Results
Once you have completed the problem, look at it again. Does your answer make sense? With the exception of two dimensional interfence patterns, you are likely to have physical experience with many wave problems. How does your answer relate to your physical experience? Can you now do steps that caused you problems earlier? Can you explain in words what is happening?
How to Solve Optics Problems
-
1.Identify the Problem

Whenever you are asked to relate what you see (the image) to an object viewed in a mirror or through a lens, you have a geometric optics problem.
-
2. Draw a Picture
The key idea to understanding where you see an image is to recognize that your brain interprets the light that reaches your eye as if the light rays travel in straight lines. Because a lens or a mirror causes the rays to change direction, you need to trace the rays that reach your eye back in straight lines. Your brain believes that they came from the location at which they (appear to) intersect.
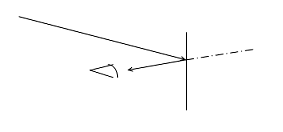
As long as you know where two points of an image are located, you know about the entire image. Therefore, we always draw part of the object on the optical axis--the corresponding point of the image is also on the axis. To locate another point of the image, we just need to look at two rays from one point of the object to see where they intersect. We traditionally draw three rays rather than two to catch mistakes. The rules for drawing the three principle rays are:
--A ray that goes to the center of the lens or mirror goes out at the same angle.
--A ray that goes in to the lens or mirror parallel to the axis goes out through the focal point.
--A ray that goes in to the lens or mirror through a focal point goes out parallel to the optical axis.
Make sure to trace each ray back to its apparent point of intersection.
-
3. Select the Relation
If you are working with a plane mirror, you only need the trigometric relationships for right triangles to solve your problem.
For circular lenses or mirrors, the key equation is
1/f = 1/o + 1/i
.In some cases, you might also need the defintion of magnification, m = hi/ho = -i/o and for mirrors the focal length is related to the radius of curvature by f = R/2.
-
4. Solve the Problem
Although the equations for geometric optics problems are mathematically straightforward, you need to understand them well to use them correctly. In particular, watch the signs on f, i, and o. Drawing a careful picture can help you catch mistakes made by incorrect use of signs. Also make sure to take the inverse (e.g. 1/o) before doing addition and to hit the "=" key before taking the inverse to find your answer. Calculators with a "1/x" key are particularly useful for geometric optics problems.
-
5. Understand the Results
Once you have completed the problem, look at it again. Does your answer make sense? You are likely to have physical experience with many optics problems. How does your answer relate to your physical experience? Can you now do steps that caused you problems earlier? Can you explain in words what is happening?
Help! I can’t find an example that looks like the problem I need to work!
-
Are you certain your problem is a Wave Physics problem?
One of the most common mistakes is to think too hard. Many of the problems that you will encounter in a unit on waves are definition problems—for example, examining the closely related quantities of wavelength and frequency. Check Definition and Ratio problems to see if you can find a useful example.
-
Yes, my problem is definitely a Wave Physics problem.
In that case, think more broadly about what makes a useful example. Remember, you were given your assignment to practice the problem solving approach, not because theanswers to your problems are particularly interesting. An example in which you merely substitute your numbers for those in the problem will give you practice entering numbers on your calculator but will teach you nothing about physics, and when you take your exam every problem on it will feel new and different to you. So think about your example as support for helping you to practice the problem solving approach.
In particular, if two problems address the same key physics they will be addressed in the same way regardless of what quantity you are asked to find. A wave going through a double slit apparatus is an interference problem even if you are asked for quantities like distance that don’t show up in the equation at all!
