
If you blow soap bubbles in sunlight, you will often see bands of color in them. What are the three smallest thicknesses of soap that will show up as red bands?
-
You may immediately recognize this as a thin film interference problem based on similar examples in your text or from lecture. But remember interference results from superposition of waves and so it is very useful to recognize this problem in the broader context of superposition.
You know that sunlight is composed of light of many different wavelengths, and each wavelength in the visible portion of the spectrum is interpreted by our brains as color. So something must happen when light hits the soap bubble to cause only some wavelengths to be seen. All colors reflect, so that "something" must be happening with the waves in the soap itself. The fact that some colors are seen and others damped out should remind you of musical instruments--some frequencies are heard and others damped out, and indeed the root physics is the same in both cases. You see (or hear) frequencies that correspond to constructively interfering waves, and you do not see or hear the frequencies corresponding to waves that cancel out.
To approach this problem, then, you need look at which wavelengths of light superpose to interfere constructively.
Waves that interfere destructively cancel out. You only see the waves with non-zero amplitude, or those that interfere constructively.
In the visible portion of the electromagnetic spectrum, frequencies correspond to color. Therefore, bands of different color represent light of different frequency (and relatedly, different wavelength.)
Any thin layer of material is considered a "thin film." In this case, the bubble is made by a very thin layer of soap with air inside. So the soap itself is the thin film.
Constructive interference happens when waves are in phase. If those waves also have the same wavelength, then they will maintain that phase relationship--if they start in phase they will stay in phase.
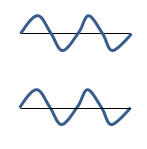
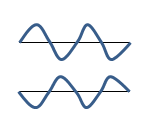
Destructive interference happens when waves are out of phase. If those waves also have the same wavelength, then they will maintain that phase relationship--if they start out of phase they will stay out of phase. Furthermore, if they are completely out of phase and have the same amplitude, they will completely cancel each other out.
Isn't this just a definition problem? Can't I just plug into the thin film equation and be done?
It is true that you have expressions for maxima and minima in thin films. However, which equation gives the max and which gives the min depends on the materials involved reflect the waves. As a result, it is best to understand the process so that you select the correct equation for your question of interest.
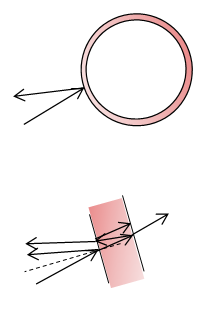
We realized above that all colors of light will reflect from the surface of the soap, and therefore realized that we need to think about interference and what happens to the light as it is in the soap itself. Therefore, your picture needs to allow room to look inside the film of soap. Furthermore, because the physics behind this problem is superposition of waves, a useful picture will show that multiple waves are present. At each interface, waves both reflect and refract, and so the lower figure shows that the incoming wave partially reflects off of the outer surface of the soap and partially refracts into the soap layer. At the inner surface there is also both reflection and refraction. This continues at each interface, although I only drew enough to show the general idea.
These drawings don't look like a soap bubble. What are you trying to show?
A soap bubble is a very thin layer of soap with air inside. Because the physics of interest takes place in that layer of soap, it is really the bottom (magnified) drawing that is useful. The top drawing just gives perspective that we are looking at the soap layer.
Why don't you show the waves themselves?
That can certainly be a useful thing to do. In that case, you know the waves that you see are the waves that are in phase, and so that part of your picture would look like:
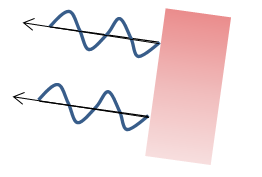
The waves that you show aren't in the same place. How do they interfere with each other?
Although it is true that the waves we consider are on top of each other, it is customary to show an exaggerated angle so that we can visualize the different waves that are present.
As I oriented this picture, you are standing to the left looking at the bubble. Therefore, the waves that get to your eye, that you see, are the waves that leave the soap bubble and travel left. I showed two of these rays. The first is reflected off of the outer surface, and the second reflected off the inner surface. As long as you know the phase relationship between these two waves, you know the phase relationship between them all.
At this interface, we can see that part of the incident wave reflects back to the observer and part of the incident wave goes into the soap.
At this interface, part of the (initially refracted) wave continues out of the soap film and into the air pocket in the bubble. Part is reflected back into the soap film. Note that this process of reflection and refraction continues each time a wave strikes an interface between air and soap.
We know that waves interfere constructively--that we will see the light--when they are in-phase.

The waves start out in phase, and so there are two factors that can change that relationship. The first is the thickness of the soap film. If one wave travels half a wavelength further than the other wave, they can end up completely out of phase and will always interfere destructively. If it travels an integer number of wavelengths further, the phase relationship (e.g. in phase) is maintained. The other factor is reflection. When a wave reflects off of an interface into a more dense medium with a higher index of refraction, the reflected wave will flip. This is the same as taking the wave 1800 out of phase.

Both effects are present in this case, and so the equation that gives an interference maximum--a bright spot--is
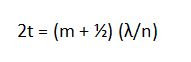
You lost me. How did you get this equation?
Click on the links, either in the discussion or on the equation. You can then find information linking each term in the equation to the understandings above.
A wave repeats after one wavelength. So if a given path difference will result in constructive interference, a path difference one, two, three, etc. wavelengths longer will also result in constructive interference. Because path length differences come about as the light travels in the soap, there are many different thickness of soap that will give constructive interference. m just numbers those thicknesses. For the three smallest wavelengths in this case, m can be 0, 1 or 2.
The light starts out as a single beam. It divides into pieces as it is reflected and refracted.
As you can see below, the waves begin with the same phase. However, the lower wave has traveled an additional half wavelength and so they are out of phase with each other.
Path differences of a full wavelength preserve the phase relationship. If two waves are in phase and one travels a full additional wavelength, they will remain in phase. The same is true if they are initially out of phase. In this case, the wave that enters the soap travels through the soap film, reflects, and travels back through the soap film. The path length difference between the two waves is twice the thickness of the soap film, or 2t.
Soap has a higher index of refraction than air. Therefore, the portion of the wave that reflects off the outer surface of the bubble will flip. The reflection off the inner surface will not flip. That means based on reflections alone the waves will be out of phase. An additional half wavelength is required in the path difference in order to bring them back to in phase.
It is the wavelength of light in soap that matters because that is where the additional travel takes place. The wavelength of a wave in material with index of refraction n is always given by the wavelength in air divided by n. (Note that your book may refer to this as λn.)In this case, n, then, refers to the index of refraction of soap.
Click on the links, either in the discussion or on the equation. You can then find information linking each term in the equation to the understandings above.
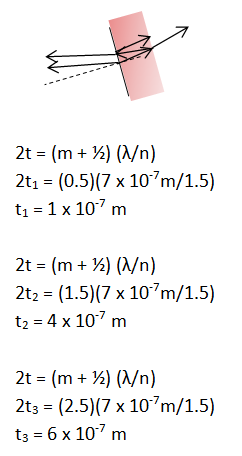
We now know the three thinnest films of soap that will give interference maxima for red light. No further solution is necessary
What is m?
The quick answer is that m is just an integer. The longer explanation is that multiple thicknesses of film will show red bands. Each additional wavelength that light travels will take the waves back to the same phase relationship. So when m = 0, the thinnest thickness that gives the result we want, the wave that goes through the soap films travels half a red wavelength farther than the wave that reflects off of the initial surface. For m = 1, the wave travels one and a half wavelengths father, etc.
I checked text books and the internet in order to find the index of refraction of soap. Values listed were between 1.3 and 1.8, so I chose to use 1.5 as a reasonable intermediate choice.
We are looking for the three thinnest soap films that will result in red bands. If the light that travels into the soap goes a total distance of one half wavelength further than the light that reflects off the surface, the waves will be back in phase after the flip upon reflection. So the thinnest soap film that gives the desired effect is for m=0, and (m + 1/2) = (0 + 1/2) = 0.5. The next time we will get a red band is when the light in the soap travels an additional one wavelength longer than that: m=1 and (m + 1/2) = (1 + 1/2) = 1.5. For the third thickness, the light travels yet one more wavelength further, for a path difference of 2.5 wavelengths.
Don't forget to divide by 2 for the final answer! (Thickness is t, not 2t.) Also note that because numbers for wavelength and index of refraction are approximate, I did not claim more than one significant figure in my answers.
You can find the wavelength of red light in your text or on the internet.
The colored bands on soap bubbles result from the interference of light. Different colors correspond to different wavelengths, and so conditions that give constructive interference for some colors will give destructive interference for other colors. In this case, the interfering waves arise because of reflection--part of the incident wave reflects off of the outer surface, part enters the soap bubble and reflects off the inner surface. This is commonly called "thin film interference."
There are two effects that affect the relative phase of the interfering waves in the case of thin films. The first is the relative path length between the waves, and the second is the possibility that the waves will be inverted on reflection from one or both interfaces. For that reason, you can't memorize an equation that gives inteference minima and one that gives interference maxima. Instead, you need to think carefully about the required path difference for your case of interest. For the soap bubble, only one of the interfaces led to inversion of the reflected wave, and so an additional half wavelength path difference is required to bring the waves into phase.
Finally, make sure that your numbers make sense. The wavelength of light is shorter inside soap than inside air, and so you expect less than half of 7 x 10-7 m for the smallest path difference, and you expect to add a number smaller than 7 x 10-7 m for each subsequent case. Don't forget that the thickness is the path difference divided by two, since the light goes across the soap film going in and again coming back out.
There are no numbers given. How do I begin this problem?
As always, begin by thinking about the key physics that causes the effect of interest. You can then look up any numbers that you need.
What causes the bands of color?
You know that sunlight is composed of light of many different wavelengths, and each wavelength in the visible portion of the spectrum is interpreted by our brains as color. The fact that some colors are seen and others damped out should remind you of musical instruments--some frequencies are heard and others damped out. The root physics is the same in both cases. You see (or hear) frequencies that correspond to constructively interfering waves.
Why does thickness matter?
This is not a question with a short answer. In order to approach it, you first need to understand that this is a standing wave (or interference) problem and then think about the equation that will correctly give constructive interference. In other words, to answer this question, pay close attention to the "Identify" and "Select the Relation" steps of the problem.
