University of Wisconsin Green Bay

• 
• Problems
• Electricity & Magnetism

Electricity & Magnetism

Electricity & Magnetism problems are often found in other categories. In addition to definition problems (e.g. electric force or field due to point charges), you use electric force in Dynamics problems and electric energy in Conservation of Energy problems. Unique to Electricity & Magnetism, however, are problems involving electric circuits or electromagnetic induction.

How to Solve Electricity and Magnetism Problems

In many cases, problems that come under Electricity and Magnetism chapters are problems you already know how to solve. These categories include Definition problems, Dynamics (force) problems, and Conservation of Energy problems. Click on these links to review the approach to solving those types of problems.

Circuit and induction problems, however, are unique to Electricity and Magnetism.

Solving Circuit Problems

• 1. Identify the Problem

  Circuit problems are very straightforward to identify. You will be given a picture or description of a combination of resistors or capacitors and asked to find the current through (or charge on) each. (Note that if you are given information about the material out of which a resistor or capacitor if made, you have a definition problem rather than a circuit problem.)

  

• 2. Draw a Picture

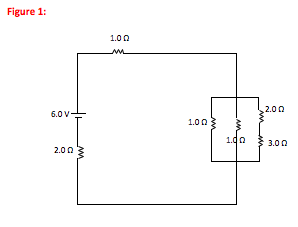
  The initial picture of the circuit is typically provided for you. However, unless you choose to use Kirchhoff’s Laws, you will need to draw a series of pictures to reduce the circuit to a single resistor (or capacitor.) Once you know this equivalent resistance (capacitance) for the entire circuit, you can find the overall effect of the battery and begin solving the problem.

  The key in circuit problems is to draw enough pictures, so that in any one step you can clearly see how that picture is a reduced version of the previous picture. If you draw the increasingly simple pictures going down the left side of your paper, this leaves you room to work each sub-problem to the right and work your way back up to the original circuit.

  To draw useful pictures, look at your current drawing and select the “innermost” combination of elements to reduce. For example, there might be resistors in series within a parallel combination. You must reduce the series of resistors before you can reduce the parallel piece. As you go from picture to picture, make sure to use the equations for equivalent resistance or capacitance to put in the correct value on your new picture.

• 3. Select the Relation

  Circuits of resistors are understood with ΔV = IR. Circuits of capacitors are understood through ΔV = Q/C.

  

• 4. Solve the Problem

  
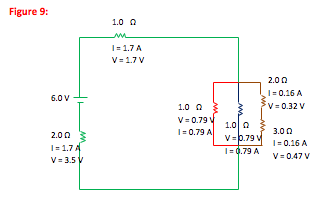
  You can use the voltage gain by the battery and the equivalent resistance (or capacitance) of the circuit to find I or Q in your simplest drawing. Then remember that current is the same for resistors in series and voltage drop is the same across resistors in parallel to work up to the more complicated drawings. Any voltage drop that you find across a “combined” parallel resistor is the same as the voltage drop across the individual resistors, allowing you to now solve for current across each. Likewise, any current you find for a “combined” series resistor is the same as the current through each of the individual resistors, allowing you to solve for voltage drop across each. Record keeping is important—any time you solve for a value, write it in on all relevant drawings.

• 5. Understand the Results

  
  

  The key ideas that you use when you work circuit problems are Conservation of Charge and Conservation of Energy.

  Conservation of Charge tells you that electrons are not used up in resistors—they merely give up some of their electric potential energy. Therefore, you can trace the path of the current in a circuit. Any region of the circuit for which there is no alternate path must have the same current, and when there are alternate paths the current in each must add up to the total.

  Conservation of Energy tells you that in the steady state of the circuit, electrons gain the same amount of potential energy as they go through the battery as the total they lose going across all resistors in their path. Therefore, as you follow any path in the circuit, you will find that that voltage gains balance the voltage drops.

  If electrons gained more energy in the battery, they would get faster—current would increase—until the total of all IRs increased enough to balance the voltage gain. If electrons gained less energy in the batter, they would slow down—current would decrease—until IRs again balanced the voltage gain.

Solving Induction Problems

• 1. Identify the Problem

  Any time you are asked about EMF or current in a loop (real or imagined), you have electromagnetic induction during any period of time in which the amount of magnetic flux through the loop changes. If there is no change, there is no induction.

• 2. Draw a Picture

  Effective pictures for induction problems show the loop(s), the magnetic field, their relative orientation, and indicate in some way what is causing the flux to change. Because these problems are typically three-dimensional, “X”s are used to indicate any vector pointing into the paper, and “ ∙ “s are used to indicate vectors pointing out of the paper.

• 3. Select the Relation

  All induction problems are understood through the relation
  EMF = -N ΔΦ/Δt = -N Δ(BA cosθ)/Δt.
  
  If you are asked to find induced current, you will also need to use EMF = IR.

  Direction of induced current is such that the induced magnetic field due to that induced current opposes the change in the original magnetic flux.

• 4. Solve the Problem:

  Typically, magnetic flux through a loop changes because either the magnetic field or the size of the loop or the orientation of the loop changes. Leave that changing quantity inside the Δ (remember, this means final value – initial value) and the math is generally straightforward to solve.

  You should relate the direction of the induced current to that of the induced magnetic field through the 2-step right hand rule.

• 5. Understand the Results

  Remember that you only have induction if the magnetic flux through a loop changes. Take a look at your problem and identify the source of the magnetic flux. Then identify what happens to cause that flux to change. Your math in solving the EMF equation should directly pair with the cause of the change in flux. If you have a closed loop, the induced EMF will result in a current through the loop, just as a battery would.

Help! I can’t find an example that looks like the problem I need to work!

Check the Definitions, Dynamics, or Energy sections. With the exception of circuits and induction, almost every problem that you will solve in your electricity and magnetism until falls under one of those three categories.

• Circuit Problems

  Circuits involving resistor and capacitors are worked with the same general approach. Differences are noted in the examples. So feel free to use an example with resistors to help work a circuit containing capacitors. In the case of capacitors, don’t follow a Kirchhoff’s Law example.

• Induction Problems

  The cause of changing flux doesn’t make a difference to how you approach induction. Any induction example will model the same approach to solving the problem.