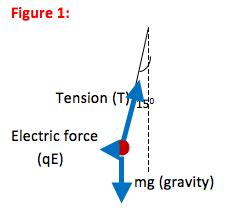
A 1.8 g (0.0018 kg) pith ball is suspended from a thread and placed in a 4500 N/C electric field. The field is directed horizontally to the left. When placed in the electric field, the pith ball is deflected to the left so that the thread makes a 15o angle with the vertical. How much charge is on the pith ball?
-
In this problem, you are asked to relate motion (the pith ball is at rest, 150 from vertical) to force (it is deflected when in the presence of an electric field). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
Nowhere in the statement of the problem are the words “force” or “acceleration” used. This is a case where your experience helps a lot! Whenever you have an equilibrium situation (in this case, static equilibrium) you know that acceleration is zero and Newton’s Second Law is a useful way to approach the problem. In addition, you know that the presence of an electric field means there is an electric force on a charged object, and the deflection of the pith ball is caused by that force. -
Step 1:
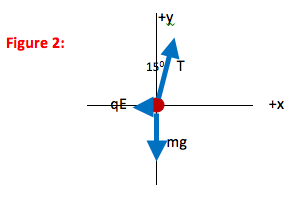
Your FBD is not yet finished, because T has both x- and y- components. Scroll down when you are ready to continue.
------------------------------------------------------------------------------
Step 2:
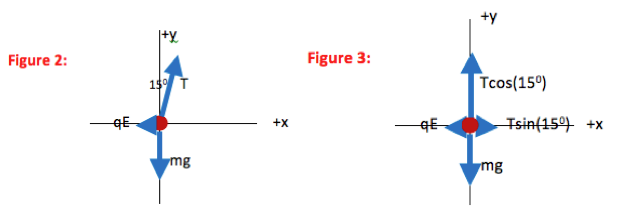
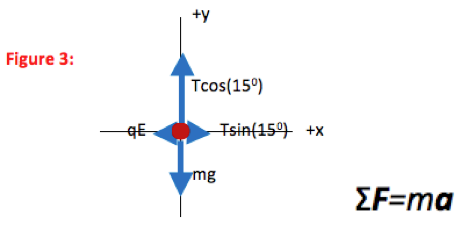
In the final FBD drawn here, all forces are divided into components. The contribution each force makes in the x-direction is shown explicitly, as is the contribution each force makes in the y-direction. The FBD is now a visual representation of ∑F=ma in each direction.
-
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
-
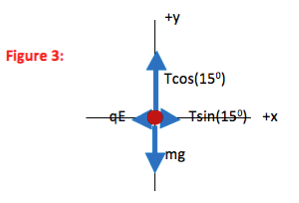
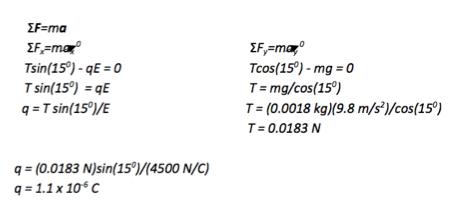
The problem asks how much charge is on the pith ball, so no further mathematical solution is needed. Because the deflection is in the same direction as the electric field (both to the left,) you know that the charge on the ball is positive. (FE = qE)
It does not matter whether you begin with the x- or the y-equation. If you solve for x first, you will need to pause in your solution to obtain a value for T from the y-equation.
Why did you pick the coordinate system to be vertical?
You can select any coordinate system that you want to use. However, the math will always be easier if you pick one axis to be in the direction of acceleration. In this case, acceleration is zero and so as a secondary consideration I used the fact that with this coordinate system I would only need to divide one force vector (tension) into components rather than two.
How did you know where to put the 15oangle?
The easiest way to approach this question is to exaggerate the small and large angles on your drawing. In other words, 15o is less than half of a right angle, so draw the angle of the thread to be very small. Then you can see that T makes a smaller angle with the +y axis than it does with the +x axis, and the smaller angle is 15o.
Why did you write “qE” for the electric force?
The presence of the electric field tells you that there is an electric force on the charged pith ball. The ball is deflected to the left. In other words, the direction of the electric force causing that deflection is to the left.
How did you divide tension into its components?
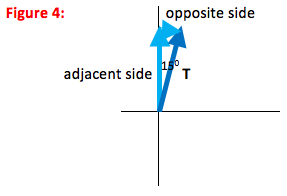
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is opposite to the 15o angle, and is given by T sin(15o) as shown. Likewise, the y-component is adjacent to the 15oangle and is therefore given by T cos(15o).Isn’t the x-component always cosθ and the y-component always sinθ?
No. Cosine goes with the component that is adjacent to θ, and sine goes with the component that is opposite to θ.

Why is 9.8 m/s2 positive?
The force of gravity acts downward, or in the -y. The negative sign is put in front of the mg in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
You could have found this example either on the Electricity and Magnetism page or on the Dynamics (force) page. If you found it by the later search, good for you! You have a good understanding of the interaction important to consider in this problem.
Whenever an object hangs from a thread (or a rope or a string), you know there is a tension force on the object. Tension is the result of the molecular attractions in the thread holding it together. Therefore, it always acts along and toward the center of the thread.
Help! How do I start?
A charged object placed in an electric field experiences (and is deflected due to) an electric force. Electric forces are treated just like any other forces, so approach the problem like any other problem in which you relate forces and motion.
Why did you pick the coordinate system to be vertical?
You can select any coordinate system that you want to use. However, the math will always be easier if you pick one axis to be in the direction of acceleration. In this case, acceleration is zero and so as a secondary consideration I used the fact that with this coordinate system I would only need to divide one force vector (tension) into components rather than two.
How did you know where to put the 15oangle?
The easiest way to approach this question is to exaggerate the small and large angles on your drawing. In other words, 15o is less than half of a right angle, so draw the angle of the thread to be very small. Then you can see that T makes a smaller angle with the +y axis than it does with the +x axis, and the smaller angle is 15o.
Why isn’t there air resistance?
The pith ball is in static equilibrium—it is at rest. Air resistance depends on the shape and velocity of an object and so if velocity is zero air resistance is also zero.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the pith ball. However, the size of the upward buoyant force compared to the downward force of gravity is small. (The ratio of the two is given by the ratio of the density of air to the density of pith.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2.
The presence of the electric field tells you that there is an electric force on the charged pith ball. The ball is deflected to the left. In other words, the direction of the electric force causing that deflection is to the left.
To locate the angle between the thread and “the vertical,” draw a vertical line that intersects with the thread. The angle between the two is the 150 angle.
In order to correctly find the 15o angle relative to the coordinate system, exaggerate the small and large angles on your drawing. In other words, 15o is less than half of a right angle, so draw the angle of the thread to be very small. Then you can see that T makes a smaller angle with the +y axis than it does with the +x axis, and the smaller angle is 15o.
No. Cosine goes with the component that is adjacent to θ, and sine goes with the component that is opposite to θ.


As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is opposite to the 15o angle, and is given by T sin(15o) as shown. Likewise, the y-component is adjacent to the 15oangle and is therefore given by T cos(15o).The electric field pushes the ball to the left, and so electric force is given a negative sign in the equation. The magnitude of the electric force on an object in an electric field is defined as qE.
Tension acts both to support the pith ball against gravity (in the +y direction in this drawing) and to balance the electric force (in the +x direction.) Only the portion of tension acting in the direction of interest should be included in the x- or y- equation. In other words, for example, the x-component of tension has no effect on how the gravitational force is balanced.
The force of gravity acts downward, or in the -y. The negative sign is put in front of the mg in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
The pith ball has been deflected to the left—it remains at rest at a 15o angle. In other words, it is in equilibrium and the acceleration of the pith ball is zero.
-
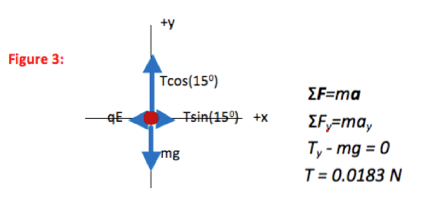
In this problem, the pith ball doesn’t fall—the vertical component of tension supports it against gravity. Knowing the geometry of the problem allows you to solve for tension in the thread directly.
-----------------------------------------------------------------------------
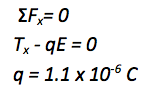
When the ball is placed in the electric field, it will swing to the left until the electric force is balanced by a horizontal component of tension.
Tension is a passive force—its value adjusts to the other forces present and to the motion of the object. Because tension must always have a vertical component to balance the weight of the ball, the tension in the rope will get larger as the ball swings to the left. (T2 = Tx2 + Ty2 = Tx2 + mg2, and Tx grows until qE is balanced.)
